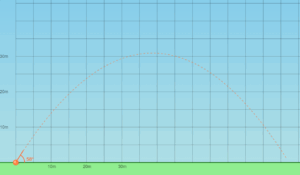
Example

Question:

A hiker stands on the edge of a cliff \(490\,\mathrm{m}\) above the ground and throws a stone horizontally with an initial speed of \(15\,\mathrm{m\,s^{-1}}\). Neglecting air resistance, find the time taken by the stone to reach the ground, and the speed with which it hits the ground. (\(g = 9.8\,\mathrm{m\,s^{-2}}\))

Solution:

Choose origin of the \(x\)- and \(y\)-axes at the edge of the cliff, \(t=0\) at throw.
Equations of motion: \[ x(t) = x_0 + v_{ox} t \] \[ y(t) = y_0 + v_{oy} t + \frac{1}{2} a_y t^2 \] Where \(x_0 = y_0 = 0\), \(v_{oy}=0\), \(a_y = -g = -9.8\,\mathrm{m\,s^{-2}}\), \(v_{ox}=15\,\mathrm{m\,s^{-1}}\)
The stone hits the ground when \(y(t) = -490\,\mathrm{m}\): \[ -490 = 0 + 0 + \frac{1}{2}(-9.8)t^2 \implies -490 = -4.9 t^2 \implies t^2 = 100 \implies t = 10\,\mathrm{s} \] Velocity components at impact: \[ v_x = v_{ox} = 15\,\mathrm{m\,s^{-1}} \] \[ v_y = v_{oy} - g t = 0 - 9.8 \times 10 = -98\,\mathrm{m\,s^{-1}} \] Speed at the ground: \[ v = \sqrt{v_x^2 + v_y^2} = \sqrt{15^2 + 98^2} = 99\,\mathrm{m\,s^{-1}} \]