Surface Tension: Droplets & Capillary Rise
Interactive simulation of spherical droplets, pressure difference, and capillary rise due to surface tension
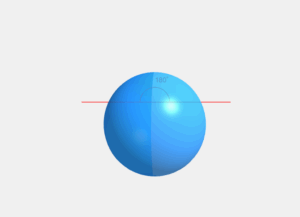
Spherical Droplet with Pressure Difference
Simulation Controls
Surface Tension (S)
0.072 N/m
Droplet Radius
2.0 mm
View Selection
Tube Radius (Capillary)
0.5 mm
Pressure Difference (ΔP)
144 Pa
Capillary Rise (h)
14.7 mm
Scientific Explanation
Spherical Droplets: A liquid minimizes its surface area to reduce surface energy. For a given volume, a sphere has the minimum surface area. This is why droplets become spherical when other forces (like gravity) are negligible.
ΔP = 2S / r
Pressure difference inside a spherical droplet (Young-Laplace equation)
Capillary Rise: Water rises in narrow tubes due to surface tension. The narrower the tube (smaller radius), the higher the rise. For a tube of radius a and contact angle θ, the height of rise is given by:
h = 2S cosθ / (ρ g a)
Jurín's law for capillary rise (θ ≈ 0° for water-glass)
Where S is surface tension, ρ is density, and g is gravitational acceleration. For water in a clean glass tube, θ ≈ 0°, so cosθ ≈ 1.