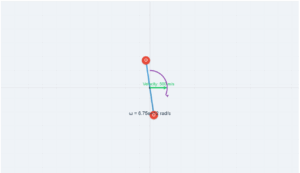
Metal Bar Equilibrium Simulation
Interactive physics demonstration of forces and moments
This simulation demonstrates the equilibrium conditions of a metal bar supported by two knife edges with a suspended load. Adjust the parameters below to explore how different configurations affect the reaction forces at the supports.
Simulation Parameters
Calculation Results
Example
Question:
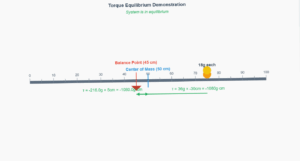
A metal bar 70 cm long and 4.00 kg in mass is supported on two knife-edges placed 10 cm from each end.
A 6.00 kg load is suspended at 30 cm from one end.
Find the reactions at the knife-edges.
(Assume the bar to be of uniform cross section and homogeneous.)
Solution:
Length of bar, \( AB = 70\,\mathrm{cm} \)
Knife edges at \( K_1 \) and \( K_2 \), both 10 cm from ends.
Mass of bar, \( M = 4.00\,\mathrm{kg} \); loaded mass \( m = 6.00\,\mathrm{kg} \) at point \( P \) (=30 cm from end A).
Centre of gravity (\( G \)) at centre (\( AG=35\,\mathrm{cm} \)), and \( AP=30\,\mathrm{cm} \), \( PG=5\,\mathrm{cm} \), \( K_1G=25\,\mathrm{cm} \), \( K_2G=25\,\mathrm{cm} \).
The weights:
\[
W = 4.00g,\quad W_1 = 6.00g
\]
where \( g = 9.8\,\mathrm{m/s}^2 \).
For translational equilibrium:
\[
R_1 + R_2 - W_1 - W = 0 \implies R_1 + R_2 = (4.00 + 6.00) \times 9.8 = 98.00\,\mathrm{N}
\]
For rotational equilibrium about \( G \):
\[
-R_1(K_1G) + W_1(PG) + R_2(K_2G) = 0
\]
Substitute values:
\[
-R_1 \times 0.25 + 6.00g \times 0.05 + R_2 \times 0.25 = 0
\]
\[
-0.25 R_1 + 2.94 + 0.25 R_2 = 0
\]
\[
R_1 - R_2 = 1.2g = 11.76\,\mathrm{N}
\]
- \( R_1 + R_2 = 98.00\,\mathrm{N} \)
- \( R_1 - R_2 = 11.76\,\mathrm{N} \)
Thus, the reactions at the supports are about \( 55\,\mathrm{N} \) at \( K_1 \) and \( 43\,\mathrm{N} \) at \( K_2 \).