Moment of a Couple Simulation
Example
Question:
Show that moment of a couple does not depend on the point about which you take the moments.
Solution:
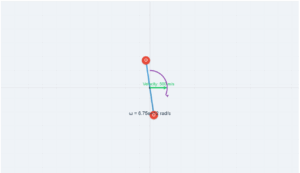
Consider a couple as shown in the figure, acting on a rigid body. The forces \( \mathbf{F} \) and \( -\mathbf{F} \) act at points \( B \) and \( A \) respectively, with position vectors \( \mathbf{r}_1 \) and \( \mathbf{r}_2 \) from the origin \( O \).
The moment of the couple is the sum of the moments of the two forces about the origin:
\[
\text{Moment} = \mathbf{r}_1 \times (-\mathbf{F}) + \mathbf{r}_2 \times \mathbf{F}
\]
\[
= \mathbf{r}_2 \times \mathbf{F} - \mathbf{r}_1 \times \mathbf{F}
\]
\[
= (\mathbf{r}_2 - \mathbf{r}_1) \times \mathbf{F}
\]
But \( \mathbf{r}_2 - \mathbf{r}_1 = \overrightarrow{AB} \), so:
\[
\text{Moment of the couple} = \overrightarrow{AB} \times \mathbf{F}
\]
This is independent of the origin—the moment does not depend on the point about which we take the moments of the forces.
Physics Explanation
A couple consists of two parallel forces that are equal in magnitude, opposite in direction, and separated by a distance.
The moment of a couple (torque) is calculated as:
M = F × d × sin(θ)
Where:
- F is the magnitude of the forces
- d is the distance between the forces
- θ is the angle between the force direction and the line connecting the points
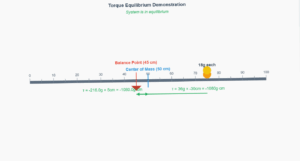
Key observation: The moment of a couple is independent of the reference point about which moments are taken, as demonstrated in this simulation.