Flywheel Physics Simulation
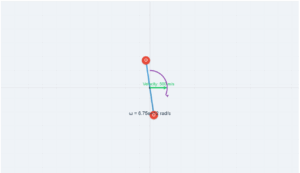
This simulation demonstrates the physics of a flywheel with a cord wrapped around it. A steady pull is applied to the cord, causing the flywheel to rotate. The simulation calculates angular acceleration, work done, and kinetic energy as described in the problem.
Flywheel Properties
Force Applied
Example
Question:
A cord of negligible mass is wound round the rim of a flywheel of mass \(20\,\mathrm{kg}\) and radius \(20\,\mathrm{cm}\). A steady pull of \(25\,\mathrm{N}\) is applied on the cord.
The flywheel is mounted on a horizontal axle with frictionless bearings.
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when \(2\,\mathrm{m}\) of the cord is unwound.
(c) Also find the kinetic energy of the wheel at this point. Assume the wheel starts from rest.
(d) Compare answers to parts (b) and (c).
Solution:
(a) The torque is:
\[
\tau = F R = 25 \times 0.20 = 5.0\,\mathrm{Nm}
\]
The moment of inertia of the flywheel,
\[
I = \frac{M R^2}{2} = \frac{20.0 \times (0.2)^2}{2} = 0.4\,\mathrm{kg\,m^2}
\]
Angular acceleration,
\[
\alpha = \frac{\tau}{I} = \frac{5.0}{0.4} = 12.5\,\mathrm{rad\,s^{-2}}
\]
(b) Work done by the pull when \(2\,\mathrm{m}\) is unwound:
\[
W = F \times s = 25 \times 2 = 50\,\mathrm{J}
\]
(c) The angular displacement is:
\[
\theta = \frac{\text{length unwound}}{\text{radius}} = \frac{2}{0.2} = 10\,\mathrm{rad}
\]
From rotational equations (starts from rest):
\[
\omega^2 = \omega_0^2 + 2 \alpha \theta, \quad \omega_0 = 0
\]
\[
\omega^2 = 2 \times 12.5 \times 10 = 250\,(\mathrm{rad/s})^2
\]
Kinetic energy gained:
\[
KE = \frac{1}{2} I \omega^2 = \frac{1}{2} \times 0.4 \times 250 = 50\,\mathrm{J}
\]
(d) Both answers are the same: the kinetic energy gained by the wheel equals the work done by the force. There is no loss of energy due to friction.