Angular Kinematics Simulation
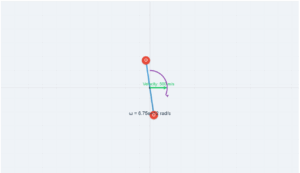
This simulation demonstrates the derivation of angular motion equations from first principles for uniformly accelerated rotation.
Initial angular velocity (ω₀):
2 rad/s
Angular acceleration (α):
1 rad/s²
Current angular velocity (ω):
2 rad/s
Angular displacement (θ):
0 rad
Derivation of Eq. (7.38) from First Principles
Given: Angular acceleration is uniform (constant)
dω/dt = α = constant
Step 1: Integrate to find angular velocity
ω = ∫α dt + C = αt + C
Step 2: Apply initial condition at t = 0, ω = ω₀
ω₀ = α(0) + C ⇒ C = ω₀
Final Equation:
ω(t) = ω₀ + αt
Extension to Angular Displacement
Using the definition ω = dθ/dt, we can integrate Eq. (7.38) to get angular displacement:
θ(t) = θ₀ + ω₀t + ½αt²
This derivation and the derivation of other angular motion equations are left as exercises.
