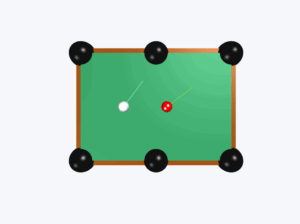
Neutron Collision Simulation
This simulation demonstrates how neutrons lose kinetic energy in elastic collisions with moderator nuclei (deuterium or carbon). The fractional energy transfer depends on the mass ratio between the neutron and moderator nucleus.
Collision Parameters
Simulation Controls
Example
Question:
Slowing down of neutrons: In a nuclear reactor, a neutron of high speed (typically \(10^7\,\mathrm{m\,s^{-1}}\)) must be slowed to \(10^3\,\mathrm{m\,s^{-1}}\) so that it can have a high probability of interacting with isotope \(^{235}U\) and causing it to fission. Show that a neutron can lose most of its kinetic energy in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a few times the neutron mass. The material making up the light nuclei, usually heavy water (\(D_2O\)) or graphite, is called a moderator.
Solution:
The initial kinetic energy of the neutron is:
\[
K_{1i} = \frac{1}{2}m_1 v_{1i}^2
\]
From elastic collision theory, the final kinetic energy is:
\[
K_{1f} = \frac{1}{2}m_1 v_{1f}^2 = \frac{1}{2}m_1 \left(\frac{m_1 - m_2}{m_1 + m_2}\right)^2 v_{1i}^2
\]
The fractional kinetic energy lost is:
\[
f_1 = \frac{K_{1f}}{K_{1i}} = \left(\frac{m_1 - m_2}{m_1 + m_2}\right)^2
\]
The fractional kinetic energy gained by the target nucleus:
\[
f_2 = 1 - f_1 = \frac{4m_1 m_2}{(m_1 + m_2)^2}
\]
For deuterium (\(m_2 = 2m_1\)):
\[
f_1 = \left(\frac{m_1 - 2m_1}{m_1 + 2m_1}\right)^2 = \left(\frac{-1}{3}\right)^2 = \frac{1}{9} \approx 11\%
\]
So \(f_2 = 1 - \frac{1}{9} = \frac{8}{9} \approx 89\%\) of the neutron's energy is transferred to deuterium.
For carbon (\(f_1 = 71.6\%\) and \(f_2 = 28.4\%\)), in practice \(f_1\) is small and head-on collisions are rare.