Spring Compression with Friction
Example
Question:
Consider Example 5.8 taking the coefficient of friction, \(\mu_s\), to be \(0.5\) and calculate the maximum compression of the spring.
Solution:
In the presence of friction, both the spring force and the frictional force act to oppose the compression of the spring.
We use the work-energy theorem. The change in kinetic energy is:
\[
\Delta K = K_f - K_i = 0 - \frac{1}{2}mv^2
\]
The work done by the net force is:
\[
W = -\frac{1}{2}kx_m^2 - \mu mg x_m
\]
Equating: \(\Delta K = W\)
\[
-\frac{1}{2}mv^2 = -\frac{1}{2}kx_m^2 - \mu mg x_m
\]
\[
\frac{1}{2}mv^2 = \frac{1}{2}kx_m^2 + \mu mg x_m
\]
Now \(\mu mg = 0.5 \times 10^3 \times 10 = 5 \times 10^3\,\mathrm{N}\) and \(\frac{1}{2}mv^2 = 1.25 \times 10^4\,\mathrm{J}\).
This gives the quadratic equation:
\[
kx_m^2 + 2\mu mg x_m - mv^2 = 0
\]
\[
5.25 \times 10^3 x_m^2 + 10^4 x_m - 2.5 \times 10^4 = 0
\]
Using the quadratic formula:
\[
x_m = \frac{-\mu mg + \sqrt{(\mu mg)^2 + mkv^2}}{k}
\]
\[
= \frac{-5 \times 10^3 + \sqrt{(5 \times 10^3)^2 + 5.25 \times 10^3 \times 2.5 \times 10^4}}{5.25 \times 10^3}
\]
\[
x_m = 1.35\,\mathrm{m}
\]
This is less than the frictionless result (\(2.0\,\mathrm{m}\)) as expected, since friction dissipates energy.
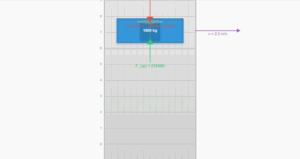
Current Compression: 0.00 m
Maximum Compression: 0.00 m