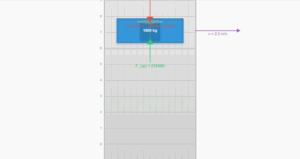
Car-Spring Collision Simulation
This simulation demonstrates the conversion of kinetic energy to spring potential energy during a collision, based on Example 6.8 from the textbook. Observe how the car's kinetic energy transforms into spring potential energy upon impact.
Example
Question:
To simulate car accidents, a car of mass \(1000\,\mathrm{kg}\) is moving with a speed \(18.0\,\mathrm{km/h}\) (\(5\,\mathrm{m/s}\)) on a smooth road and collides with a horizontally mounted spring of spring constant \(5.25 \times 10^3\,\mathrm{N\,m^{-1}}\). What is the maximum compression of the spring?
Solution:
At maximum compression, the car's kinetic energy is completely converted to the spring's potential energy.
Kinetic energy of car:
\[
K = \frac{1}{2}mv^2 = \frac{1}{2} \times 1000 \times 5^2 = 1.25 \times 10^4\,\mathrm{J}
\]
At maximum compression \(x_m\),
\[
V = \frac{1}{2}k x_m^2 = K
\]
\[
\frac{1}{2} \times 5.25 \times 10^3 \times x_m^2 = 1.25 \times 10^4
\]
\[
x_m^2 = \frac{2 \times 1.25 \times 10^4}{5.25 \times 10^3} = \frac{2.5 \times 10^4}{5.25 \times 10^3} \approx 4.76
\]
\[
x_m = 2.00\,\mathrm{m}
\]
Assumptions: Spring is massless, surface has negligible friction.
Physics Explanation:
From the textbook example with a 1000 kg car moving at 18 km/h (5 m/s) and spring constant k = 6.25 × 10³ N/m:
K = ½mv² = ½ × 1000 kg × (5 m/s)² = 12500 J
All kinetic energy converts to spring potential energy:
V = ½kxm² = K
xm = √(2K/k) = √(2 × 12500 / 6250) = 2 m
The simulation shows how the car's kinetic energy is gradually converted to the spring's potential energy during the collision, with the total mechanical energy remaining constant (conservation of energy).
E = K + V = constant
At any point during collision: ½mv² + ½kx² = ½mv₀²