Example

Question:

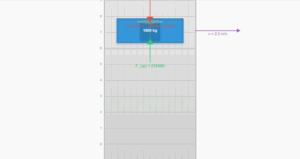
A block of mass \(m = 1\,\mathrm{kg}\), moving on a horizontal surface with speed \(v_i = 2\,\mathrm{m\,s^{-1}}\), enters a rough patch ranging from \(x = 0.10\,\mathrm{m}\) to \(x = 2.01\,\mathrm{m}\). The retarding force \(F_r\) on the block in this range is inversely proportional to \(x\) over this range: \[ F_r = -\frac{k}{x} \text{ for } 0.1 < x < 2.01\,\mathrm{m} \] where \(k = 0.5\,\mathrm{J}\).
What is the final kinetic energy and speed \(v_f\) of the block as it crosses this patch?

Solution:

From the work-energy theorem: \[ K_f = K_i + \int_{0.1}^{2.01} \left(-\frac{k}{x}\right) dx \] \[ = \frac{1}{2} m v_i^2 - k \ln(x) \Big|_{0.1}^{2.01} \] \[ = \frac{1}{2} m v_i^2 - k \ln\left( \frac{2.01}{0.1} \right) \] Substitute \(m = 1\,\mathrm{kg},\, v_i = 2\,\mathrm{m\,s^{-1}},\, k = 0.5\,\mathrm{J}\): \[ = 2 - 0.5 \ln(20.1) \] \[ \approx 2 - 0.5 \times 3.0 = 2 - 1.5 = 0.5\,\mathrm{J} \] The final speed: \[ v_f = \sqrt{2K_f/m} = \sqrt{2 \times 0.5 / 1} = 1\,\mathrm{m\,s^{-1}} \] Note: ln here is the natural logarithm (base \(e\)), not base 10.