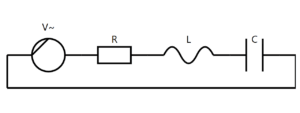
RLC Circuit Simulator
Example
Question:
A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series LCR circuit in which \(R = 3\,\Omega\), \(L = 25.48\,\text{mH}\), and \(C = 796\,\mu\text{F}\). Find
(a) the impedance of the circuit;
(b) the phase difference between the voltage across the source and the current;
(c) the power dissipated in the circuit;
(d) the power factor.
Solution:
(a) Inductive reactance:
\[
X_L = 2\pi\nu L = 2 \times 3.14 \times 50 \times 25.48 \times 10^{-3} = 8\,\Omega
\]
Capacitive reactance:
\[
X_C = \frac{1}{2\pi\nu C} = \frac{1}{2 \times 3.14 \times 50 \times 796 \times 10^{-6}} = 4\,\Omega
\]
Therefore,
\[
Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{3^2 + (8-4)^2} = 5\,\Omega
\]
(b) Phase difference:
\[
\phi = \tan^{-1} \left(\frac{X_C - X_L}{R}\right) = \tan^{-1}\left(\frac{4-8}{3}\right) = -53.1^\circ
\]
Since \(\phi\) is negative, current lags voltage across the source.
(c) Power dissipated:
\[
P = I^2 R
\]
Now,
\[
I = \frac{i_m}{\sqrt{2}} = \frac{1}{\sqrt{2}} \left(\frac{283}{5}\right) = 40\,\text{A}
\]
\[
P = (40)^2 \times 3 = 4800\,\text{W}
\]
(d) Power factor:
\[
\cos\phi = \cos(-53.1^\circ) = 0.6
\]