Electromagnetic Induction Simulation
Example 6.5: Faraday's Law Demonstrations
Part (a): Stationary Loop in Magnetic Field
Can we generate current in a stationary loop between strong magnets?
Solution: No. However strong the magnet may be, current can be induced only by changing the magnetic flux through the loop.
ε = -dΦB/dt (Faraday's Law)
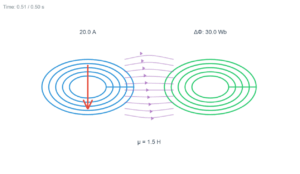
The induced electromotive force (emf) in any closed circuit is equal to the negative of the time rate of change of the magnetic flux through the circuit.
Part (b): Loop in Capacitor's Electric Field
Is current induced when moving through a capacitor's electric field?
Solution: No current is induced in either case. Current cannot be induced by changing the electric flux.
Faraday's law relates to changing magnetic flux, not electric flux. This demonstrates that electric and magnetic fields have different effects on charge motion.
Part (c): Rectangular vs Circular Loop Exiting Field
Which loop maintains constant induced emf when exiting a uniform field?
Solution: The induced emf is expected to be constant only in the case of the rectangular loop. In the circular loop, the rate of change of area during exit isn't constant.
ε = -B(dA/dt) (For constant B and v)
The rectangular loop exits the field at a constant rate (dA/dt is constant), while the circular loop's area changes non-linearly as it exits, resulting in varying emf.
Part (d): Capacitor Polarity Prediction
Predict the polarity of the capacitor in the given situation.
Solution: The polarity of plate 'A' will be positive with respect to plate 'B' in the capacitor.
This is determined by Lenz's Law, which states that the direction of induced current will oppose the change in magnetic flux that produced it. The current flows in a direction to create a magnetic field opposing the increasing flux through the loop.
