12th Class Exercise 7.6

LC Oscillation Circuit Simulation

Natural Frequency: 177 Hz

Angular Frequency: 1111 rad/s

Period: 5.65 ms

Total Energy: 16.7 µJ

Charge Q(t): 1.00 mC

Current I(t): 0.00 A

V_C(t): 33.3 V

V_L(t): 0.0 V

Simulation Controls

Circuit Parameters

Inductance (mH)

27 mH

Capacitance (µF)

30 µF

Initial Charge (mC)

1.0 mC

Animation Speed

1.0x

Animation Control

Simulation Control

Energy Analysis

Electric Energy (Capacitor)

16.7 µJ

U_E = Q²/(2C)

Magnetic Energy (Inductor)

0.0 µJ

U_B = LI²/2

Total Energy

16.7 µJ

U_total = U_E + U_B

Real-time Waveforms

Charge Q(t)

Current I(t)

V_C(t)

V_L(t)

Understanding LC Oscillations

Energy Conservation

In an ideal LC circuit, total energy is conserved. Energy oscillates between electric energy stored in the capacitor and magnetic energy stored in the inductor.

U_total = Q_max²/(2C) = LI_max²/2 = constant

Natural Frequency

The natural frequency of LC oscillations depends only on the inductance L and capacitance C values, not on the initial charge or energy.

f = 1/(2π√(LC))

ω = 1/√(LC)

Phase Relationships

Charge Q(t) and capacitor voltage V_C(t) are in phase. Current I(t) leads charge by 90°, being maximum when charge is zero.

Q(t) = Q_max cos(ωt)

I(t) = -ωQ_max sin(ωt)

Voltage Relationship

At any instant, the sum of voltages across the inductor and capacitor equals zero, since there is no external voltage source.

V_C(t) + V_L(t) = 0

V_C(t) = Q(t)/C

V_L(t) = -L(dI/dt)

Mechanical Analogy

LC oscillations are analogous to a mass-spring system: L ↔ mass, 1/C ↔ spring constant, Q ↔ displacement, I ↔ velocity.

                        • Capacitor stores electric energy (like a spring)

                        • Inductor stores magnetic energy (like kinetic energy)

                        • Current flows back and forth (like oscillating motion)

                        • Natural frequency is determined by L and C

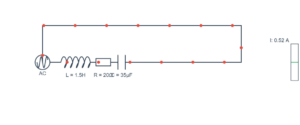
Problem 7.6 Solution

For the circuit with L = 27mH and C = 30µF:

ω = 1/√(LC) = 1/√(27×10⁻³ × 30×10⁻⁶) = 1111 rad/s

f = ω/(2π) = 1111/(2π) = 177 Hz

T = 2π/ω = 2π/1111 = 5.65 ms