De Broglie Bohr Model: Interactive Quantum Mechanics
This interactive physics simulation demonstrates how the de Broglie Bohr model elegantly combines wave-particle duality with quantized electron orbits. When Louis de Broglie proposed that electrons behave as waves, he provided a profound explanation for Bohr's empirical quantization rules. The simulation shows standing waves forming around the nucleus, where only specific wavelengths create stable, non-destructive interference patterns.
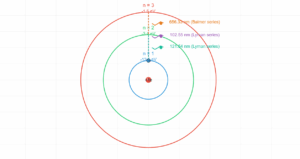
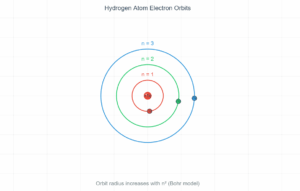
In the de Broglie Bohr model, electrons can only occupy orbits where an integer number of wavelengths fits perfectly into the orbital circumference (2πr = nλ). This standing wave condition naturally leads to quantized angular momentum and explains why atoms have discrete energy levels. Use the controls below to explore different quantum numbers and see how the wave patterns change.
Understanding Quantum Orbits
The simulation above visualizes one of the most elegant connections in quantum mechanics. De Broglie's hypothesis that matter has wave properties provided the missing piece to understand why Bohr's atomic model worked. When an electron forms a standing wave around the nucleus, only certain discrete orbits are stable—those where the wave connects smoothly with itself after one complete revolution.
This quantum behavior explains atomic stability and the discrete spectral lines observed in atomic emission spectra. Each allowed orbit corresponds to a specific energy level, and transitions between these levels produce photons with characteristic wavelengths.