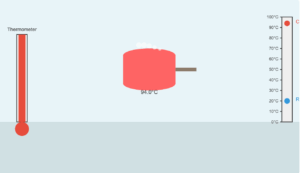
Thermal Junction Simulation
Visualizing heat transfer through steel and copper rods between a furnace and ice box
Steel Rod Parameters
Copper Rod Parameters
Example
Question:
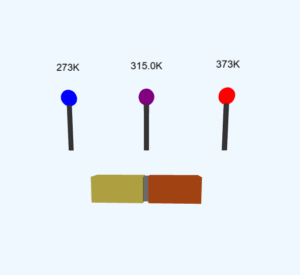
An iron bar (\(L_1 = 0.1\,\mathrm{m}\), \(A_1 = 0.02\,\mathrm{m}^2\), \(K_1 = 79\,\mathrm{W\,m^{-1}\,K^{-1}}\)) and a brass bar (\(L_2 = 0.1\,\mathrm{m}\), \(A_2 = 0.02\,\mathrm{m}^2\), \(K_2 = 109\,\mathrm{W\,m^{-1}\,K^{-1}}\)) are soldered end to end as shown. The free ends of the iron and brass bars are maintained at \(373\,\mathrm{K}\) and \(273\,\mathrm{K}\) respectively. Obtain expressions for and compute:
(i) the temperature of the junction of the two bars,
(ii) the equivalent thermal conductivity of the compound bar,
(iii) the heat current through the compound bar.
Solution:
Under steady-state, heat current is equal through each bar:
\[
H = H_1 = H_2 = \frac{K_1 A_1 (T_1 - T_0)}{L_1} = \frac{K_2 A_2 (T_0 - T_2)}{L_2}
\]
For \(A_1 = A_2 = A\), \(L_1 = L_2 = L\):
\[
K_1(T_1 - T_0) = K_2(T_0 - T_2)
\]
\[
T_0 = \frac{K_1 T_1 + K_2 T_2}{K_1 + K_2}
\]
Substituting given values:
\[
T_0 = \frac{79 \times 373 + 109 \times 273}{79 + 109}
= 315\,\mathrm{K}
\]
The equivalent thermal conductivity,
\[
K' = \frac{2 K_1 K_2}{K_1 + K_2}
\]
\[
K' = \frac{2 \times 79 \times 109}{79 + 109} = 91.6\,\mathrm{W\,m^{-1}\,K^{-1}}
\]
Heat current through the compound bar,
\[
H = H' = \frac{K' A (T_1 - T_2)}{2L}
\]
\[
= \frac{91.6\,\mathrm{W\,m^{-1}\,K^{-1}} \times 0.02\,\mathrm{m}^2 \times (373-273)\,\mathrm{K}}{2 \times 0.1\,\mathrm{m}}
= 916.1\,\mathrm{W}
\]