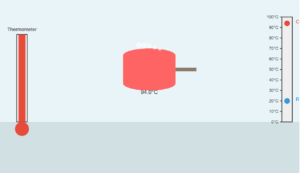
Thermal Expansion: Iron Ring on Wooden Wheel
Example
Question:
A blacksmith fixes an iron ring on the rim of the wooden wheel of a horse cart. The diameter of the rim and the iron ring are 5.243 m and 5.231 m, respectively, at 27°C. To what temperature should the ring be heated so as to fit the rim of the wheel?
Solution:
Given,
\[
T_1 = 27^\circ\mathrm{C}
\]
\[
L_{T_1} = 5.231\,\mathrm{m}
\]
\[
L_{T_2} = 5.243\,\mathrm{m}
\]
The formula for linear expansion is:
\[
L_{T_2} = L_{T_1}[1 + \alpha_l(T_2 - T_1)]
\]
Substituting the values,
\[
5.243 = 5.231[1 + 1.20 \times 10^{-5}\,\mathrm{K^{-1}}(T_2 - 27)]
\]
Solving,
\[
T_2 = 218^\circ\mathrm{C}
\]
Physics Explanation
This simulation demonstrates the thermal expansion of an iron ring that needs to fit onto a wooden wheel rim. The ring must be heated to expand its diameter to match the wheel.
Where:
- LT1 = Initial length at temperature T1 (5.231 m)
- LT2 = Length at temperature T2 (5.243 m)
- α = Coefficient of linear expansion for iron (1.20 × 10-5 K-1)
- T1 = Initial temperature (27°C)
- T2 = Final temperature
Calculation Results
Required expansion: 5.243 m - 5.231 m = 0.012 m (12 mm)
Required temperature increase: ΔT = 191°C (from 27°C to 218°C)