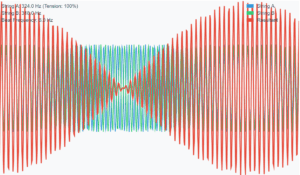
Transverse Wave Physics Simulation
Explore how tension and mass affect wave speed on a string
10 N
60 N
100 N
1 g
5 g
10 g
0.5 m
0.72 m
1.5 m
0.5 Hz
2 Hz
5 Hz
Example
Question:
A steel wire \(0.72\,\mathrm{m}\) long has a mass of \(5.0 \times 10^{-3}\,\mathrm{kg}\).
If the wire is under a tension of \(60\,\mathrm{N}\), what is the speed of transverse waves on the wire?
Solution:
Mass per unit length:
\[
\mu = \frac{5.0 \times 10^{-3}\,\mathrm{kg}}{0.72\,\mathrm{m}} = 6.9 \times 10^{-3}\,\mathrm{kg\,m^{-1}}
\]
Tension: \(T = 60\,\mathrm{N}\)
Speed of wave:
\[
v = \sqrt{\frac{T}{\mu}} = \sqrt{\frac{60}{6.9\times10^{-3}}} = 93\,\mathrm{m\,s^{-1}}
\]
Wave Physics Relationships
Wave speed on a string is given by:
v = √(T/μ)
Where:
- v = wave speed (m/s)
- T = tension in the string (N)
- μ = mass per unit length (kg/m)
Key Relationships:
- Wave speed increases with increasing tension
- Wave speed decreases with increasing mass
- Wave speed is independent of frequency or amplitude
Current wave speed: 93 m/s (μ = 6.9 × 10⁻³ kg/m, T = 60 N)