Wave Equation Simulation
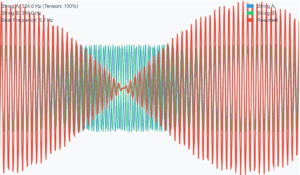
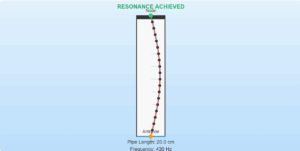
This simulation visualizes the wave described by the equation: y(x, t) = 0.005 sin(80.0x - 3.0t) from Example 15.2. You can observe the wave's characteristics and track a specific point's displacement.
Example
Question:
A wave travelling along a string is described by
\( y(x, t) = 0.005 \sin (80.0\,x - 3.0\,t) \),
where all quantities are in SI units.
(a) Calculate the amplitude, (b) the wavelength, (c) the period and frequency of the wave. Also, calculate the displacement \( y \) of the wave at \( x = 30.0\,\mathrm{cm} \) and \( t = 20\,\mathrm{s} \).
Solution:
(a) Amplitude: \( a = 0.005\, \mathrm{m} = 5\,\mathrm{mm} \)
(b) Angular wave number: \( k = 80.0\,\mathrm{m^{-1}} \), angular frequency \( \omega = 3.0\,\mathrm{s^{-1}} \)
Wavelength:
\[
\lambda = \frac{2\pi}{k} = \frac{2\pi}{80.0} = 0.0785\,\mathrm{m} = 7.85\,\mathrm{cm}
\]
(c) Period:
\[
T = \frac{2\pi}{\omega} = \frac{2\pi}{3.0} = 2.09\,\mathrm{s}
\]
Frequency:
\[
f = \frac{1}{T} = 0.48\,\mathrm{Hz}
\]
Displacement at \( x = 0.3\,\mathrm{m},\, t = 20\,\mathrm{s} \):
\[
y = 0.005 \sin [80.0 \times 0.3 - 3.0 \times 20]
= 0.005 \sin (24.0 - 60.0)
= 0.005 \sin (-36.0)
= 0.005 \sin (-36 + 12\pi)
= 0.005 \sin (1.699)
\approx 0.005 \times 0.99 = 0.00495\,\mathrm{m} \approx 5\,\mathrm{mm}
\]