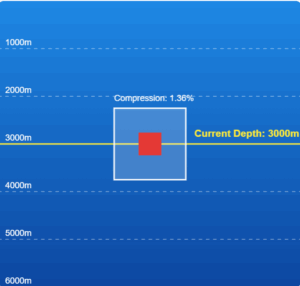
Wire Stretching Simulation
A copper wire (2.2m) and steel wire (1.6m) connected end-to-end, both with diameter 3.0mm, are stretched by a load. Adjust the parameters below to see how the wires behave.
Example
Question:
A copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied.
Solution:
The copper and steel wires are under a tensile stress because they have the same tension (equal to the load \(W\)) and the same area of cross-section \(A\).
From Eq. (8.7), stress = strain × Young's modulus:
\[
\frac{W}{A} = Y_c\left(\frac{\Delta L_c}{L_c}\right) = Y_s\left(\frac{\Delta L_s}{L_s}\right)
\]
where subscripts \(c\) and \(s\) refer to copper and steel respectively.
Or,
\[
\frac{\Delta L_c}{\Delta L_s} = \left(\frac{Y_s}{Y_c}\right)\left(\frac{L_c}{L_s}\right)
\]
Given \(L_c = 2.2\,\mathrm{m}\), \(L_s = 1.6\,\mathrm{m}\), \(Y_s = 2.0 \times 10^{11}\,\mathrm{N\,m}^{-2}\), \(Y_c = 1.1 \times 10^{11}\,\mathrm{N\,m}^{-2}\):
\[
\frac{\Delta L_c}{\Delta L_s} = \left(\frac{2.0 \times 10^{11}}{1.1 \times 10^{11}}\right)\left(\frac{2.2}{1.6}\right) = 2.5
\]
The total elongation is
\[
\Delta L_c + \Delta L_s = 7.0 \times 10^{-4}\,\mathrm{m}
\]
Solving above,
\[
\Delta L_c = 5.0 \times 10^{-4}\,\mathrm{m},\quad \Delta L_s = 2.0 \times 10^{-4}\,\mathrm{m}
\]
Therefore,
\[
W = \frac{A Y_c \Delta L_c}{L_c}
= \pi (1.5 \times 10^{-3})^2 \frac{[5.0 \times 10^{-4} \times 1.1 \times 10^{11}]}{2.2}
= 1.8 \times 10^2\,\mathrm{N}
\]