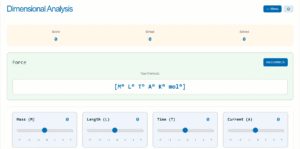
Semiconductor Doping Simulation
Example
Question:
Suppose a pure Si crystal has \(5 \times 10^{28}\) atoms m\(^{-3}\). It is doped by 1 ppm concentration of pentavalent As. Calculate the number of electrons and holes. Given that \( n_i = 1.5 \times 10^{16} \) m\(^{-3}\).
Solution:
Thermally generated electrons (\( n_i \sim 10^{16} \) m\(^{-3}\)) are negligible compared to those produced by doping.
Therefore, \( n_e \approx N_D \).
Since \( n_e n_h = n_i^2 \), the number of holes:
\[
n_h = \frac{n_i^2}{n_e} = \frac{(1.5 \times 10^{16})^2}{5 \times 10^{22}}
= \frac{2.25 \times 10^{32}}{5 \times 10^{22}}
= 4.5 \times 10^9~\text{m}^{-3}
\]
Carrier Concentration Calculations
Given: Pure Si crystal has 5×1028 atoms/m3
Doped with 1 ppm As (pentavalent)
Donor concentration (ND) = 5×1022 m-3
Intrinsic concentration (ni) = 1.5×1016 m-3
Electron concentration (ne) ≈ ND = 5×1022 m-3
Hole concentration (nh) = ni2/ND = 4.5×109 m-3