Maximum Focal Length Problem
Interactive demonstration of how lens position affects required focal length in a constrained optical system
Lens Position Control
Real-time Calculations
Lens Equation Applied:
1/f = 1/u + 1/v → 1/0.75 = 1/1.50 + 1/1.50
Focal Length vs Lens Position
Physics Insights
Maximum Focal Length Principle
fmax = d/4 = 3/4 = 0.75 m
Maximum focal length occurs when the lens is positioned at the center, equidistant from both object and image (u = v = 1.5 m).
Mathematical Derivation
With constraint u + v = d = 3m:
f = uv/(u+v) = u(3-u)/3
Maximum when df/du = 0 → u = 1.5m
Symmetrical Configuration
When u = v = 1.5m, the lens-object-image system is perfectly symmetrical, minimizing optical aberrations and maximizing the possible focal length.
Practical Applications
• Projector Design: Optimal lens placement
• Camera Systems: Fixed distance focusing
• Optical Benches: Educational demonstrations
• Telescope Design: Constrained configurations
Textbook Problem Solution
Problem Setup
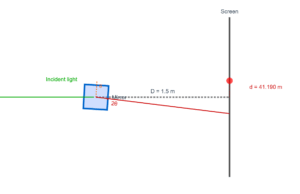
Given: Electric bulb on one wall, image screen on opposite wall, 3 meters apart
Find: Maximum possible focal length of convex lens
Constraint Analysis
Constraint: u + v = 3m (fixed wall separation)
Lens Equation: 1/f = 1/u + 1/v
Focal Length: f = uv/(u+v)
Optimization
Substitute constraint: f = u(3-u)/3
Maximize: df/du = (3-2u)/3 = 0
Solution: u = 1.5m → fmax = 0.75m
Physical Interpretation
Maximum focal length of 0.75m occurs when lens is centered at 1.5m from each wall. Any other position requires a shorter focal length lens.