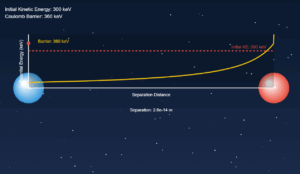
Nuclear Matter Density Simulation
This simulation demonstrates the constant nature of nuclear matter density. The relationship between nuclear radius (R) and mass number (A) is given by:
\[ R = R_0 A^{\frac{1}{3}} \]
Where \( R_0 \) is the radius constant (~1.2 fm). The density remains constant because volume increases proportionally with mass.
1
50
250
0.5 fm
1.2 fm
2.0 fm
Nuclear Physics Formulas
Nuclear radius: \( R = R_0 A^{\frac{1}{3}} \)
Nuclear volume: \( V = \frac{4}{3}\pi R^3 = \frac{4}{3}\pi R_0^3 A \)
Nuclear density: \( \rho = \frac{mA}{V} = \frac{3m}{4\pi R_0^3} \)
Current values:
- Mass number (A): 50
- Radius constant (R₀): 1.2 fm
- Nuclear radius (R): 4.15 fm
- Nuclear density (ρ): 0.138 nucleons/fm³