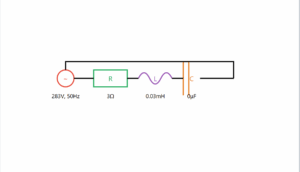
RC Circuit in AC
This simulation demonstrates an RC circuit connected to an AC source as described in Example 7.6, showing the phase relationship between voltages.
Impedance (Z)
Z = √(R² + XC²)
Current (I)
I = V/Z
VR (rms)
VR = IR
VC (rms)
VC = IXC
Capacitive Reactance
XC = 1/(2πνC)
Phase Angle
φ = tan-1(-XC/R)
Example
Question:
A resistor of \(200\,\Omega\) and a capacitor of \(15.0\,\mu\text{F}\) are connected in series to a \(220\,\text{V},\ 50\,\text{Hz}\) AC source.
(a) Calculate the current in the circuit.
(b) Calculate the voltage (rms) across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltage? If yes, resolve the paradox.
Solution:
Given: \(R = 200\,\Omega,\ C = 15.0\,\mu\text{F} = 15.0 \times 10^{-6}\text{F},\ V = 220\,\text{V},\ \nu = 50\,\text{Hz}\)
(a) Impedance:
\[
Z = \sqrt{R^2 + X_C^2} = \sqrt{R^2 + (2\pi \nu C)^{-2}}
\]
\[
Z = \sqrt{(200)^2 + (212.3)^2} = 291.67\,\Omega
\]
Current:
\[
I = \frac{V}{Z} = \frac{220}{291.67} = 0.755\,\text{A}
\]
(b) Voltage across resistor:
\[
V_R = I R = 0.755 \times 200 = 151\,\text{V}
\]
Voltage across capacitor:
\[
V_C = I X_C = 0.755 \times 212.3 = 160.3\,\text{V}
\]
Algebraic sum \(V_R + V_C = 311.3\,\text{V}\), which is more than the source voltage (\(220\,\text{V}\)).
Resolution: The voltages are not in the same phase; they must be added via Pythagoras:
\[
V_{R+C} = \sqrt{V_R^2 + V_C^2} = 220\,\text{V}
\]
Thus, the total matches the source voltage when phase is accounted for.
Explanation (from Example 7.6):
This simulation shows an RC circuit with R = 200Ω and C = 15μF connected to a 220V, 50Hz AC source.
Key observations:
- The algebraic sum of VR (151V) and VC (160.3V) is 311.3V, which exceeds the source voltage (220V)
- This apparent paradox is resolved by recognizing the voltages are 90° out of phase
- The actual total voltage is the vector sum: V = √(VR² + VC²) = 220V
- The current leads the source voltage by 46.7° (phase angle)