3D Mutual Inductance of Concentric Coils
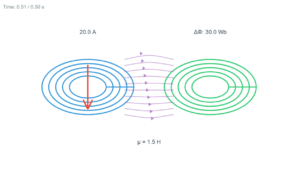
Two concentric circular coils, one of small radius r₁ and the other of large radius r₂ (r₁ << r₂), are placed co-axially with centers coinciding. Obtain the mutual inductance of the arrangement.
\[M_{12} = M_{21} = \frac{\mu_0 \pi r_1^2}{2r_2}\]
Interactive 3D Simulation
Explore how mutual inductance changes with coil dimensions in 3D:
Example
Question:
Two concentric circular coils, one of small radius \( r_1 \) and the other of large radius \( r_2 \), such that \( r_1 \ll r_2 \), are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
Solution:
Let a current \( I_2 \) flow through the outer circular coil. The field at the centre of the coil is:
\[
B_2 = \frac{\mu_0 I_2}{2 r_2}
\]
Since the small co-axially placed coil has radius \( r_1 \ll r_2 \), \( B_2 \) may be considered constant over its cross-sectional area:
Flux through small coil:
\[
\Phi_1 = \pi r_1^2 B_2 = \pi r_1^2 \left( \frac{\mu_0 I_2}{2 r_2} \right) = \frac{\mu_0 \pi r_1^2}{2 r_2} I_2
\]
Thus,
\[
M_{12} = \frac{\mu_0 \pi r_1^2}{2 r_2}
\]
From symmetry, \( M_{21} = M_{12} \).
Note: This is valid since \( r_1 \ll r_2 \) and \( B_2 \) is nearly uniform over small coil area.