Wheel Spoke EMF Simulation
Example 6.7
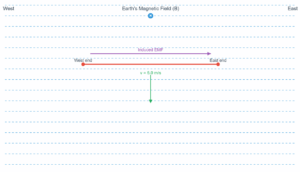
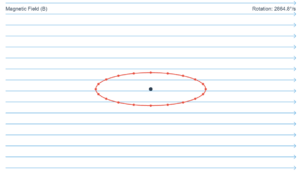
A wheel with 10 metallic spokes each 0.5 m long is rotated at 120 rev/min in Earth's magnetic field (HE = 0.4 G). What is the induced emf between the axle and the rim?
Induced emf:
\[\varepsilon = \frac{1}{2} \omega B R^2\]
\[= \frac{1}{2} \times 4\pi \times 0.4 \times 10^{-4} \times (0.5)^2\]
\[= 6.28 \times 10^{-5} \, \text{V}\]
\[\varepsilon = \frac{1}{2} \omega B R^2\]
\[= \frac{1}{2} \times 4\pi \times 0.4 \times 10^{-4} \times (0.5)^2\]
\[= 6.28 \times 10^{-5} \, \text{V}\]
Interactive Simulation
Explore how rotation in Earth's magnetic field induces EMF in wheel spokes:
EMF direction: from rim to axle
120 rev/min
0.5 m
0.4 G
10 spokes
Angular Velocity (ω)
12.57 rad/s
Induced EMF (ε)
6.28 × 10-5 V
Magnetic Field (B)
0.4 × 10-4 T
