3D Rotating Rod in Magnetic Field
Example 6.6: EMF in a Rotating Rod (3D Simulation)
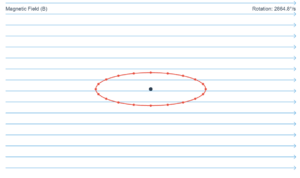
A metallic rod of 1 m length rotates at 50 rev/s, with one end hinged at the center and the other end at the circumference of a circular metallic ring of radius 1 m. A uniform magnetic field of 1 T parallel to the axis is present everywhere.
Example
Question:
A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular to the plane of the ring (Fig. 6.11). A constant and uniform magnetic field of 1 T parallel to the axis is present everywhere. What is the emf between the centre and the metallic ring?
Solution:
Method I:
As the rod rotates, free electrons move outward due to Lorentz force, producing an emf. The magnitude across the ends is
\[
d\epsilon = B v\ dr
\]
Since \(v = \omega r\),
\[
\epsilon = \int_{0}^{R} B \omega r\ dr = B\omega \int_{0}^{R} r\ dr = \frac{1}{2} B \omega R^2
\]
For \(B=1,\ \omega=2\pi \times 50,\ R=1\):
\[
\epsilon = \frac{1}{2} \times 1 \times 2\pi \times 50 \times 1^2 = 157\ \text{V}
\]
Method II:
Using rate of change of area swept out:
\[
\text{Area} = \frac{1}{2} R^2 \theta
\]
\[
\epsilon = B \frac{d}{dt}\left(\frac{1}{2} R^2 \theta\right) = \frac{1}{2} B R^2 \frac{d\theta}{dt} = \frac{1}{2} B \omega R^2
\]
Both methods yield:
\[
\epsilon = 157\ \text{V}
\]
As the rod rotates, free electrons move towards the outer end due to Lorentz force, creating an emf:
EMF equals B × (rate of change of area of loop):