Example

Question:

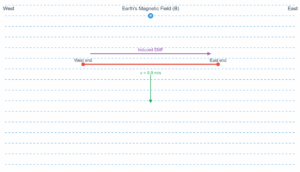
A square loop of side 10 cm and resistance 0.5 Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10 T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70 s at a steady rate. Determine the magnitudes of induced emf and current during this time-interval.

Solution:

The angle \(\theta\) between the area vector and magnetic field is \(45^\circ\).
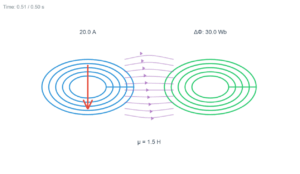
Initial magnetic flux: \[ \Phi = B A \cos\theta = \frac{0.1 \times 10^{-2}}{\sqrt{2}}\ \text{Wb} \] Final flux: \(\Phi_{\text{min}} = 0\)
The change in flux occurs in \(0.70\,\text{s}\):
Induced emf magnitude: \[ \epsilon = \left|\frac{\Delta \Phi_B}{\Delta t}\right| = \frac{| \Phi - 0 |}{\Delta t} = \frac{10^{-3}}{\sqrt{2} \times 0.7}\ \text{V} = 1.0\ \text{mV} \] Induced current magnitude: \[ I = \frac{\epsilon}{R} = \frac{10^{-3}}{0.5} = 2\ \text{mA} \] The earth's field also produces steady flux, but does not induce any emf here.