Magnetic Energy in Solenoid: 3D Simulation
(a) Obtain the expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length l of the solenoid.
(b) Compare this magnetic energy with the electrostatic energy stored in a capacitor.
\[U_B = \frac{1}{2\mu_0} B^2 Al\]
Magnetic energy density:
\[u_B = \frac{B^2}{2\mu_0}\]
Electrostatic energy density:
\[u_E = \frac{1}{2} \epsilon_0 E^2\]
The magnetic energy stored in a solenoid is analogous to the electric energy stored in a capacitor. Both represent energy stored in their respective fields.
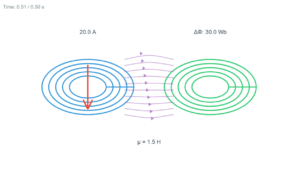
3D Interactive Simulation
Adjust the parameters below to explore how magnetic energy is stored in a solenoid. Rotate and zoom the 3D visualization with your mouse/touch.
Energy Storage Comparison
The energy density in a magnetic field depends on the square of the magnetic field strength (B) and the magnetic permeability of free space (μ₀):
For our solenoid with B = 0.05 T:
For comparison with a capacitor (E = 5.0 × 10⁵ V/m):
\[u_E = \frac{1}{2}(8.854×10^{-12})(5.0 × 10⁵)^2= 1.11 \text{ J/m}^3\]
This comparison shows that while the forms are similar, the actual energy densities depend on the field strengths and the fundamental constants μ₀ and ε₀, which are related through the speed of light: μ₀ε₀ = 1/c².
