Magnetic Field Around a Current-Carrying Wire
Simulation of magnetic field inside and outside a wire with uniform current distribution
Example
Question:
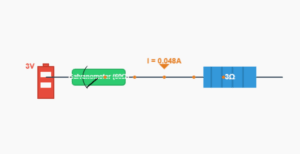
Figure 4.13 shows a long straight wire of a circular cross-section (radius \(a\)) carrying steady current \(I\). The current \(I\) is uniformly distributed across this cross-section. Calculate the magnetic field in the region \(r < a\) and \(r > a\).
Solution:
(a) For \(r > a\):
The Amperian loop is concentric with the cross-section. The current enclosed by the loop is \(I\).
The magnetic field at distance \(r\) (outside the wire) is
\[
B = \frac{\mu_0 I}{2\pi r}
\]
so \( B \propto \frac{1}{r} \) for \( r > a \).
(b) For \( r < a \) (inside the wire):
The current enclosed is only a fraction of total current:
\[
I_e = I \frac{\pi r^2}{\pi a^2} = I\frac{r^2}{a^2}
\]
By Ampère’s law,
\[
B(2\pi r) = \mu_0 I \frac{r^2}{a^2}
\implies B = \frac{\mu_0 I}{2\pi a^2} r
\]
so \( B \propto r \) for \( r < a \).
Figure 4.14 shows the plot: \(B\) rises linearly for \(r < a\), then decreases as \(1/r\) for \(r > a\).
Physics Explanation
For a long straight wire with radius a carrying current I uniformly distributed:
Inside the wire (r < a):
B = (μ₀I / 2πa²) * r
Magnetic field increases linearly with distance from center.
Outside the wire (r > a):
B = μ₀I / 2πr
Magnetic field decreases inversely with distance from center.
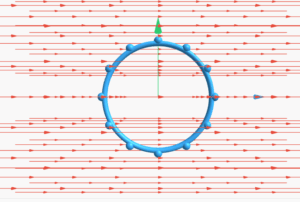
The direction of the field is always tangential to circular loops around the wire, following the right-hand rule.