Semi-Circular Current Magnetic Field
Example 4.6: Magnetic Field of Bent Wire
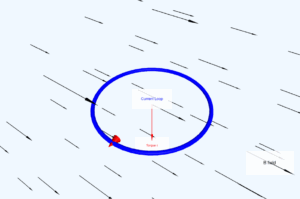
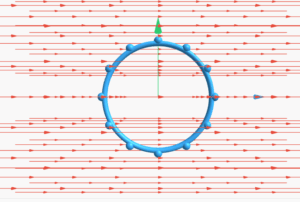
This simulation demonstrates the magnetic field at the center of a semi-circular current-carrying wire.
Example
Question:
A straight wire carrying a current of 12 A is bent into a semi-circular arc of radius 2.0 cm as shown in Fig. 4.11(a). Consider the magnetic field \(\mathbf{B}\) at the centre of the arc.
(a) What is the magnetic field due to the straight segments?
(b) In what way the contribution to \(\mathbf{B}\) from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semi-circular arc of the same radius but in the opposite way as shown in Fig. 4.11(b)?
Solution:
(a) \(d\mathbf{l}\) and \(\mathbf{r}\) for each element of the straight segments are parallel. Therefore, \(d\mathbf{l} \times \mathbf{r} = 0\). Straight segments do not contribute to \(|\mathbf{B}|\).
(b) For all segments of the semicircular arc, \(d\mathbf{l} \times \mathbf{r}\) are all parallel to each other (into the plane of the paper). All such contributions add up in magnitude. Hence direction of \(\mathbf{B}\) for a semicircular arc is given by the right-hand rule and magnitude is half that of a circular loop. Thus \(\mathbf{B} = 1.9 \times 10^{-4}\,\text{T}\), normal to the plane of the paper into it.
(c) Same magnitude of \(\mathbf{B}\) but opposite in direction to that in (b).
Key Concepts
Right-Hand Rule
Curl fingers in current direction, thumb points in field direction (into plane for scenario a, out of plane for scenario b).