Example

Question:

An element \(\Delta \mathbf{l} = \Delta x \mathbf{\hat{i}}\) is placed at the origin and carries a large current \(I = 10\,\text{A}\) (Fig. 4.8). What is the magnetic field on the \(y\)-axis at a distance of \(0.5\,\text{m}\)? \(\Delta x = 1\,\text{cm}\).

Solution:

\[ |\mathbf{dB}| = \frac{\mu_0}{4\pi} \frac{I\,d\ell\,\sin\theta}{r^2} \] where \(d\ell = \Delta x = 10^{-2}\,\text{m}\), \(I = 10\,\text{A}\), \(r = 0.5\,\text{m}\), \(\mu_0/4\pi = 10^{-7}\,\text{Tm/A}\).
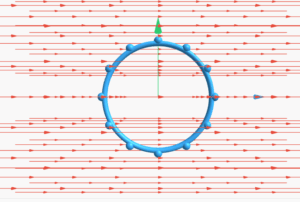
\(\theta = 90^\circ\), so \(\sin\theta = 1\). \[ |\mathbf{dB}| = \frac{10^{-7}\times10\times10^{-2}}{25\times10^{-2}} = 4 \times 10^{-8}\,\text{T} \] The direction is in the \(+\mathbf{\hat{k}}\) (z-axis) direction: \[ d\mathbf{l} \times \mathbf{r} = \Delta x\mathbf{\hat{i}} \times y\mathbf{\hat{j}} = y\Delta x\,\mathbf{\hat{k}} \] Note, the field is small in magnitude.