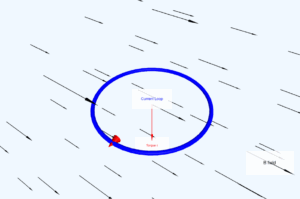
3D Magnetic Coil Simulation
This interactive 3D simulation demonstrates Example 4.10, showing the behavior of a current-carrying coil in a magnetic field.
Simulation
(a) Field at Center:
2 × 10⁻³ T (direction given by right-hand rule)
(b) Magnetic Moment:
10 A·m² (direction given by right-hand rule)
(c) Torques:
Initial torque (θ=0°): 0 N·m
Final torque (θ=90°): 20 N·m
(d) Angular Speed:
20 rad/s (when rotated by 90°)
Key Equations:
Magnetic field at center: \( B = \frac{\mu_0 NI}{2R} \)
Magnetic moment: \( m = NIA = NIπr^2 \)
Torque: \( \tau = mB\sinθ \)
Angular speed: \( \omega = \sqrt{\frac{2mB}{I}} \)
Solution to Example 4.10
Question:
A 100 turn closely wound circular coil of radius 10 cm carries a current of 3.2 A.
(a) What is the field at the centre of the coil?
(b) What is the magnetic moment of this coil?
The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of 2 T in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through angle of 90° under the influence of the magnetic field.
(c) What are the magnitudes of the torques on the coil in the initial and final position?
(d) What is the angular speed acquired by the coil when it has rotated by 90°? The moment of inertia of the coil is 0.1 kg m².
(a) Field at Center:
\[ B = \frac{\mu_0 NI}{2R} \]
Given: \( N=100 \), \( I=3.2 \) A, \( R=0.1 \) m
\[ B = \frac{4π×10^{-7}×100×3.2}{2×0.1} = 2×10^{-3} \text{ T} \]
Direction given by right-hand thumb rule.
(b) Magnetic Moment:
\[ m = NIA = NIπr^2 \]
\[ m = 100×3.2×3.14×10^{-2} = 10 \text{ A·m}^2 \]
Direction given by right-hand thumb rule.
(c) Torques:
\[ \tau = mB\sinθ \]
Initial (θ=0°): \( \tau_i = 10×2×\sin0° = 0 \text{ N·m} \)
Final (θ=90°): \( \tau_f = 10×2×\sin90° = 20 \text{ N·m} \)
(d) Angular Speed:
From work-energy principle:
\[ \frac{1}{2}I\omega^2 = mB(1-\cos90°) \]
\[ \frac{1}{2}×0.1×\omega^2 = 10×2×1 \]
\[ \omega = \sqrt{\frac{2×20}{0.1}} = 20 \text{ rad/s} \]