3D Cubical Resistor Network Simulation
This interactive 3D simulation demonstrates Example 3.6, showing current distribution in a cubical network of 12 identical resistors.
Simulation
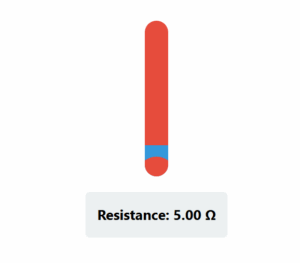
Current in Each Resistor:
Equivalent Resistance Calculation:
\[ \varepsilon = \frac{5}{2}IR \]
\[ R_{eq} = \frac{\varepsilon}{3I} = \frac{5}{6}R \]
For \( R = 1 \Omega \), \( R_{eq} = \frac{5}{6} \Omega \)
Solution to Example 3.5
Question:
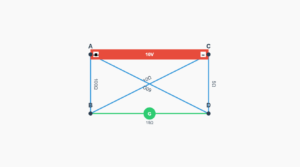
A battery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance \(1\,\Omega\) (Fig. 3.16). Determine the equivalent resistance of the network and the current along each edge of the cube.
The network is not reducible to simple series and parallel combinations of resistors. We exploit the symmetry in the problem:
The paths AA', AD and AB are symmetrically placed. Current in each must be the same (I).
At corners A', B and D, the incoming current I splits equally into two outgoing branches (I/2).
Applying Kirchhoff's second rule to loop ABCC'EA:
\[ -IR - \frac{1}{2}IR - IR + \varepsilon = 0 \]
\[ \varepsilon = \frac{5}{2}IR \]
Equivalent resistance:
\[ R_{eq} = \frac{\varepsilon}{3I} = \frac{5}{6}R \]
For \( R = 1 \Omega \), \( R_{eq} = \frac{5}{6} \Omega \)
For \( \varepsilon = 10 \) V, total current \( 3I = \frac{10}{5/6} = 12 \) A
Thus, \( I = 4 \) A and branch currents are as shown.