Example

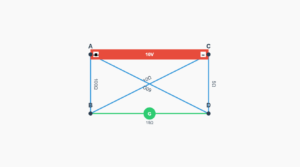
Question:

An electric toaster uses nichrome for its heating element. When a negligibly small current passes through it, its resistance at room temperature (\(27.0^\circ \text{C}\)) is found to be \(75.3\,\Omega\). When the toaster is connected to a \(230\,\text{V}\) supply, the current settles, after a few seconds, to a steady value of \(2.68\,\text{A}\). What is the steady temperature of the nichrome element? The temperature coefficient of resistance of nichrome averaged over the temperature range involved, is \(1.70 \times 10^{-4}\,^\circ\text{C}^{-1}\).

Solution:

When a small current passes, heating effects are negligible and the temperature \(T_1\) is room temperature.
When connected to supply, initial current is slightly higher, but heating causes temperature to rise and resistance to increase, current slightly decreases until steady state.
The steady resistance is \[ R_2 = \frac{230\,\text{V}}{2.68\,\text{A}} = 85.8\,\Omega \] Using \(R_2 = R_1[1+\alpha(T_2-T_1)]\) with \(\alpha = 1.70 \times 10^{-4}\,^\circ\text{C}^{-1}\): \[ T_2 - T_1 = \frac{85.8 - 75.3}{75.3 \times 1.70 \times 10^{-4}} = 820^\circ\text{C} \] Thus, \[ T_2 = (820 + 27.0)\,^\circ\text{C} = 847^\circ\text{C} \] Therefore, the steady temperature of the heating element is \(847^\circ \text{C}\).