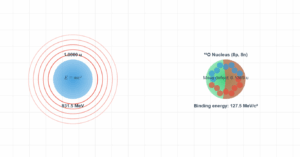
Nuclear Density Simulation
Compare the extreme density of atomic nuclei with neutron stars ℹ️ Pinch to zoom on mobile devices
Example
Question:
Given the mass of iron nucleus as 55.85u and \(A=56\), find the nuclear density.
Solution:
\( m_{\rm{Fe}} = 55.85\,\text{u} \), \( \text{u} = 9.27 \times 10^{-26}\,\text{kg} \)
Nuclear density:
\[
\text{density} = \frac{\text{mass}}{\text{volume}} =
\frac{9.27 \times 10^{-26}}{(4\pi/3)(1.2 \times 10^{-15})^3} \times \frac{1}{56}
= 2.29 \times 10^{17}~\text{kg m}^{-3}
\]
The density of matter in neutron stars is comparable to this value, showing such objects are as compressed as a big nucleus.
Iron nucleus density: 2.29 × 1017 kg/m³
Neutron star density: ~3.7 × 1017 kg/m³
Water density (comparison): 1 × 103 kg/m³