Hydrogen Atom Electron Orbit
Example
Question:
According to the classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
Solution:
From Example 12.3, the velocity of the electron moving around a proton in a hydrogen atom with radius \( 5.3 \times 10^{-11} \) m is \( 2.2 \times 10^6 \) m/s. Thus, the frequency of revolution: \[ \nu = \frac{v}{2\pi r} = \frac{2.2 \times 10^6~\text{m/s}}{2\pi \times 5.3 \times 10^{-11}~\text{m}} \approx 6.6 \times 10^{15}~\text{Hz} \] According to classical electromagnetic theory, the frequency of light emitted is equal to the electron's revolution frequency. Thus, the initial frequency of light emitted is \( 6.6 \times 10^{15}~\text{Hz} \).
Calculated Values:
Orbital frequency: 6.6 × 10¹⁵ Hz
Emitted light frequency: 6.6 × 10¹⁵ Hz
Wavelength: 45.5 nm (Ultraviolet)
Physics Explanation:
According to classical electromagnetic theory:
- An electron orbiting a nucleus is an accelerating charge
- Accelerating charges emit electromagnetic radiation
- The frequency of emitted radiation equals the orbital frequency
The orbital frequency is calculated using:
ν = v / (2πr)
where:
- ν = frequency (Hz)
- v = electron velocity (m/s)
- r = orbit radius (m)
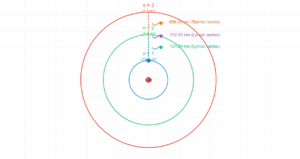
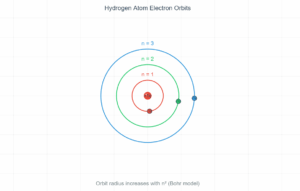
For hydrogen atom (ground state):
- Radius (r) = 5.3 × 10⁻¹¹ m
- Velocity (v) = 2.2 × 10⁶ m/s
- Calculated frequency = 6.6 × 10¹⁵ Hz (UV region)