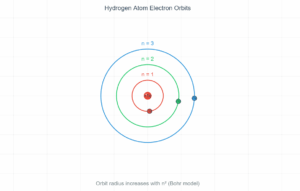
Hydrogen Atom Simulation with Speed Control
Example
Question:
It is found experimentally that 13.6 eV energy is required to separate a hydrogen atom into a proton and an electron. Compute the orbital radius and the velocity of the electron in a hydrogen atom.
Solution:
The total energy of the electron in hydrogen atom is \(-13.6~\text{eV} = -13.6 \times 1.6 \times 10^{-19}~\text{J} = -2.2 \times 10^{-18}~\text{J}\). Using the formula: \[ E = -\frac{e^2}{8\pi\epsilon_0 r} \] Substituting values, \[ r = \frac{e^2}{8\pi\epsilon_0 E} = \frac{(9 \times 10^9~\text{N m}^2/\text{C}^2)(1.6 \times 10^{-19}~\text{C})^2}{2 \times (-2.2 \times 10^{-18}~\text{J})} = 5.3 \times 10^{-11}~\text{m} \] The velocity is \[ v = \frac{e}{\sqrt{4\pi\epsilon_0 m r}} = 2.2 \times 10^{6}~\text{m/s} \]
Hydrogen Atom Properties
The total energy of an electron in a hydrogen atom is given by:
E = -13.6 eV / n²
Where n is the principal quantum number.
Current values:
- Quantum level (n): 1
- Orbital radius: 5.3 × 10⁻¹¹ m
- Electron velocity: 2.2 × 10⁶ m/s
- Energy: -13.6 eV (-2.2 × 10⁻¹⁸ J)
- Animation speed: 1.0×