Atomic Charge Distribution
Interactive Simulation
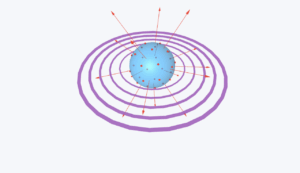
This simulation visualizes the electric field in an atom model with a positive nucleus and uniform negative charge distribution.
Example
Question:
An early model for an atom considered it to have a positively charged point nucleus of charge \( Ze \), surrounded by a uniform density of negative charge up to a radius \( R \). The atom as a whole is neutral. For this model, what is the electric field at a distance \( r \) from the nucleus?
Solution:
The total negative charge in the uniform spherical charge distribution of radius \( R \) must be \( -Ze \). Hence the negative charge density \( \rho \) is
\[
4\pi R^3 / 3 \cdot \rho = -Ze \implies \rho = -\frac{3Ze}{4\pi R^3}
\]
To find the electric field \( \mathbf{E}(r) \) at a point \( P \) a distance \( r \) from the nucleus, use Gauss's law.
The charge \( q \) enclosed by a spherical Gaussian surface of radius \( r \) is
\[
q = Ze + \frac{4\pi r^3}{3} \rho
\]
Substitute \( \rho \):
\[
q = Ze - Ze \frac{r^3}{R^3}
\]
By Gauss's law,
\[
E(r) = \frac{Ze}{4\pi\varepsilon_0} \frac{1}{r^2} \left(1 - \frac{r^3}{R^3} \right), \quad \text{for } r < R
\]
For \( r > R \), the total enclosed charge is zero (since the atom is neutral), so
\[
E(r) = 0 \quad \text{for } r > R
\]
At \( r = R \), both formulas yield \( E = 0 \).
Results
Explanation
The example models an atom with:
- Point nucleus with charge +Ze
- Uniform negative charge distribution (radius R) with total charge -Ze
- Overall neutral atom
Key Concepts:
Charge Density: ρ = -3Ze/(4πR³) (Uniform negative charge distribution)
Gauss's Law: ∮E·dA = q_enclosed/ε₀
Electric Field Calculation:
For r < R: E(r) = Ze/(4πε₀)(1/r² - r/R³)
- First term: Nuclear contribution (1/r²)
- Second term: Electron cloud contribution (linear in r)
For r > R: E(r) = 0 (Atom is neutral, no external field)
At r = R: Field is continuous and E(R) = 0