Interactive Hydrogen Atom Energy Level Diagram
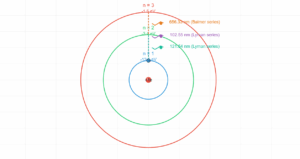
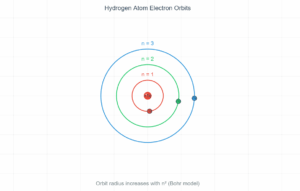
This interactive simulation demonstrates the quantized energy levels of a hydrogen atom according to Bohr's atomic model. In quantum mechanics, electrons can only occupy specific discrete energy states rather than any arbitrary energy value. The hydrogen atom energy level diagram below visualizes these distinct energy states, with the lowest energy state (n=1) representing the ground state.
Understanding energy quantization is fundamental to modern physics. When electrons absorb energy, they jump to higher energy levels (excited states). Conversely, when electrons release energy, they transition downward, emitting photons with specific wavelengths corresponding to the energy difference between levels.
Understanding Quantum Energy Levels
The hydrogen atom energy level diagram reveals one of nature's most elegant patterns. Each energy level is characterized by the principal quantum number (n), which can only take positive integer values (1, 2, 3, ...). This quantization means electrons cannot exist between these levels—they must "jump" from one to another.
Key Concepts to Remember
- Ground State: The lowest energy configuration (n=1) where the electron is closest to the nucleus
- Excited States: Higher energy levels (n≥2) where the electron has absorbed energy
- Energy Absorption: Moving upward requires energy input (photon absorption)
- Energy Emission: Moving downward releases energy as light (photon emission)
- Ionization: Providing enough energy to completely free the electron from the atom
Applications in Physics Education
This visualization serves as an excellent complement to hands-on laboratory work. Just as a thermal expansion experiment demonstrates how materials change dimensions with temperature variations, this simulation shows how energy affects atomic behavior. Both concepts illustrate fundamental physical principles through observable changes.
Students can use this tool to predict spectral lines, understand atomic spectra, and grasp why hydrogen produces its characteristic colors when excited. The discrete energy transitions shown here explain why we see specific wavelengths of light rather than a continuous spectrum.