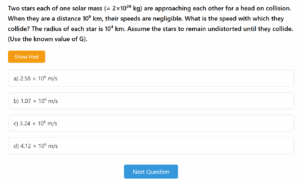
Planetary Orbit Comparison
Visualizing Kepler's Third Law with a planet orbiting twice as fast as Earth
Orbital Parameters
Earth's Orbital Period:
1.0 year
Planet's Orbital Period:
0.5 years
Earth's Orbital Radius:
1.0 AU
Planet's Orbital Radius:
0.63 AU
Physics Explanation
Using Kepler's Third Law of Planetary Motion:
(Rₚ/Rₑ)³ = (Tₚ/Tₑ)²
Where:
- Rₚ = orbital radius of the planet
- Rₑ = orbital radius of Earth (1 AU)
- Tₚ = orbital period of the planet (0.5 years)
- Tₑ = orbital period of Earth (1 year)
Solving for the planet's orbital radius:
Rₚ = Rₑ × (Tₚ/Tₑ)^(2/3) = 1 AU × (0.5)^(2/3) ≈ 0.63 AU
This shows that a planet orbiting twice as fast as Earth would have an orbital radius about 0.63 times Earth's distance from the Sun.