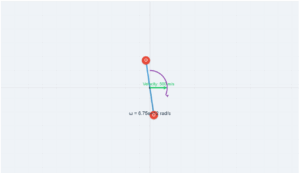
Center of Gravity Simulation
Interactive demonstration of center of mass calculation
0 (Center)
0.5
1 (Edge)
Original Disk
Cutout Hole
Original Center
Hole Center
Center of Gravity
Physics Explanation
This simulation demonstrates the center of gravity (centroid) of a uniform disk with a circular hole cut out.
Problem Statement: From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The center of the hole is at a distance d = R/2 from the center of the original disk.
Solution: The center of gravity is located at R/6 from the original center, opposite to the center of the cut portion.
Mathematical Derivation:
Mass of original disk: M = σπR²
Mass of removed hole: m = σπ(R/2)² = M/4
Center of mass (x-coordinate): x_cm = (M×0 - m×d)/(M - m) = -(M/4 × R/2)/(3M/4) = -R/6