Angular Momentum Conservation
Demonstration of rotational kinetic energy changes
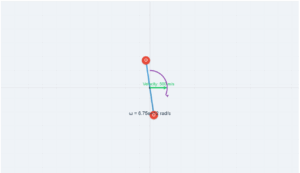
Angular Velocity
0
rev/min
Moment of Inertia
1.0
I₀ (relative)
Kinetic Energy
0
J (relative)
Physics Explanation
This simulation demonstrates the conservation of angular momentum and the change in rotational kinetic energy when a child pulls their arms in while rotating on a turntable.
Problem Statement: A child stands at the center of a turntable with arms outstretched, rotating at 40 rev/min. When the child folds their arms, reducing their moment of inertia to 2/5 of the initial value, what is the new angular speed?
Solution:
- Initial angular velocity: ω₁ = 40 rev/min
- Moment of inertia ratio: I₂ = (2/5)I₁
- Conservation of angular momentum: I₁ω₁ = I₂ω₂
- Final angular velocity: ω₂ = (I₁/I₂)ω₁ = (5/2) × 40 = 100 rev/min
Kinetic Energy Change:
Rotational kinetic energy is given by KE = ½Iω².
Initial KE: KE₁ = ½I₁ω₁²
Final KE: KE₂ = ½I₂ω₂² = ½(2/5)I₁ × (5/2 ω₁)² = (5/2) × ½I₁ω₁² = 2.5 × KE₁
The kinetic energy increases because the child does work to pull their arms inward against the centrifugal force.