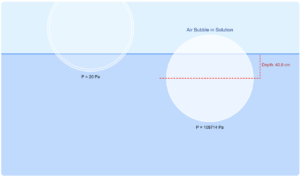
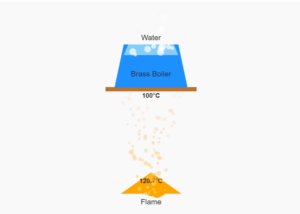
Copper-Ice Thermal Energy Transfer
Simulation of heat transfer and phase change
Copper Mass (m)
2.5 kgMass of the copper block
Copper Temperature (ΔT)
500°CInitial temperature of copper
Heat Transfer
Melted Ice Mass
1.45 kgAmount of ice melted by copper's heat
Thermodynamic Principles
Q = m·C·ΔT = mice·Lf
- Q: Heat energy transferred (J)
- m: Mass of copper block (g)
- C: Specific heat of copper (0.39 Jg⁻¹K⁻¹)
- ΔT: Temperature change of copper (K or °C)
- mice: Mass of ice melted (g)
- Lf: Heat of fusion of water (335 Jg⁻¹)
Current heat transfer: 487,500 J
Maximum ice melted: 1.45 kg (1,455.22 g)
Maximum ice melted: 1.45 kg (1,455.22 g)
This simulation demonstrates heat transfer from a hot copper block to ice, causing the ice to melt. The copper block loses heat energy (Q = m·C·ΔT) which is gained by the ice to overcome its latent heat of fusion (Q = mice·Lf).
The specific heat capacity of copper (0.39 Jg⁻¹K⁻¹) determines how much energy it releases as it cools, while the heat of fusion of water (335 Jg⁻¹) determines how much ice can be melted with that energy.