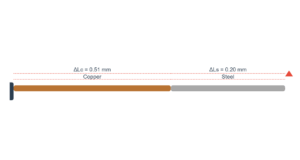
Shear Deformation Simulation
Example
Question:
A square lead slab of side 50 cm and thickness 10 cm is subject to a shearing force (on its narrow face) of \(9.0 \times 10^4\,\mathrm{N}\). The lower edge is riveted to the floor. How much will the upper edge be displaced?
Solution:
The lead slab is fixed and the force is applied parallel to the narrow face.
The area of the face parallel to which this force is applied:
\[
A = 50\,\mathrm{cm} \times 10\,\mathrm{cm} = 0.5\,\mathrm{m} \times 0.1\,\mathrm{m} = 0.05\,\mathrm{m}^2
\]
The stress applied is:
\[
\text{Stress} = \frac{9.4 \times 10^4\,\mathrm{N}}{0.05\,\mathrm{m}^2} = 1.80 \times 10^6\,\mathrm{N\,m}^{-2}
\]
Shearing strain is given by:
\[
\frac{\Delta x}{L} = \frac{\text{Stress}}{G}
\]
Therefore, the displacement:
\[
\Delta x = \frac{\text{Stress} \times L}{G}
= \frac{1.8 \times 10^6\,\mathrm{N\,m}^{-2} \times 0.5\,\mathrm{m}}{5.6 \times 10^9\,\mathrm{N\,m}^{-2}}
= 1.6 \times 10^{-4}\,\mathrm{m} = 0.16\,\mathrm{mm}
\]
Example 9.4
A square lead slab of side 50 cm and thickness 10 cm is subject to a shearing force (on its narrow face) of 9.0 × 10⁴ N. The lower edge is riveted to the floor. How much will the upper edge be displaced?
Area (A) = 50 cm × 10 cm = 0.05 m²
Stress = F/A = (9.0 × 10⁴ N) / (0.05 m²) = 1.8 × 10⁶ N/m²
Displacement Δx = (Stress × L)/G
= (1.8 × 10⁶ N/m² × 0.5 m) / (5.6 × 10⁹ N/m²)
= 1.6 × 10⁻⁴ m = 0.16 mm