Sitar Strings Beat Frequency Simulation
Example 14.6
Two sitar strings A and B playing the note 'Dha' are slightly out of tune and produce beats of frequency 5 Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease to 3 Hz. What is the original frequency of B if the frequency of A is 427 Hz?
Answer: The original frequency of B is 422 Hz.
How It Works
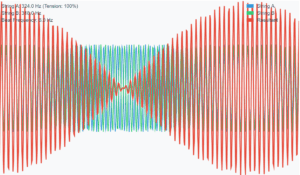
This simulation demonstrates the beat frequency phenomenon that occurs when two sound waves of slightly different frequencies interfere with each other.
- String A is fixed at 427 Hz (as in the problem).
- String B starts at 422 Hz, creating a 5 Hz beat frequency (427 - 422 = 5).
- When you increase String B's tension, its frequency increases, reducing the beat frequency.
- The waves combine to create a pulsing "beat" effect shown in the visualization.
- Click "Play Sound" to hear the sitar strings and their beat pattern.
