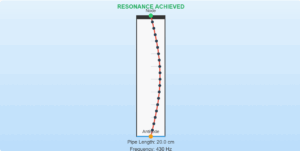
Pipe Harmonics Resonance Simulator
Example
Question:
A pipe, \(30.0\,\mathrm{cm}\) long, is open at both ends. Which harmonic mode of the pipe resonates a \(1.1\,\mathrm{kHz}\) source? Will resonance with the same source be observed if one end of the pipe is closed? Take the speed of sound in air as \(330\,\mathrm{m\,s^{-1}}\).
Solution:
Open at both ends:
For an open pipe, first harmonic frequency:
\[
v_1 = \frac{v}{2L}
\]
nth harmonic:
\[
v_n = \frac{n v}{2L}, \quad n = 1, 2, 3, \dots
\]
Here \(L = 0.30\,\mathrm{m}\), \(v = 330\,\mathrm{m/s}\):
\[
v_n = \frac{n \times 330}{2 \times 0.30} = \frac{n \times 330}{0.6} = 550n \ \mathrm{Hz}
\]
For \(v_2 = 2 \times 550 = 1100\,\mathrm{Hz} = 1.1\,\mathrm{kHz}\): resonant with the source at the second harmonic.
One end closed:
For a pipe closed at one end, fundamental frequency:
\[
v_1 = \frac{v}{4L}
\]
Only odd harmonics:
\[
v_3 = \frac{3v}{4L}, \quad v_5 = \frac{5v}{4L}, \dots
\]
Here \(v_1 = \frac{330}{4 \times 0.30} = \frac{330}{1.2} = 275\,\mathrm{Hz}\)
\(1.1\,\mathrm{kHz}\) would correspond to the fourth harmonic if all were allowed: \(275 \times 4 = 1100\,\mathrm{Hz}\). But only odd harmonics are possible, so no resonance at this frequency with one end closed.
Physics of Pipe Harmonics
This simulation demonstrates standing wave patterns in pipes with different boundary conditions:
Closed-Closed Pipe: Both ends are Closed (antinodes)
fn = n × v / (4L) (n = 1, 2, 3...)
Closed-Open Pipe: One open end (antinode), one closed end (node)
fn = n × v / (2L) (n = 1, 3, 5...)
Current harmonic frequency: 330 Hz
Resonance with source: No