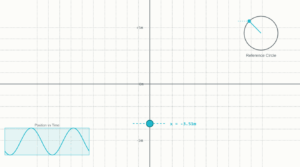
Simple Harmonic Motion Simulation
Interactive demonstration of mass-spring oscillator
System Parameters
Simulation Controls
Example
Question:
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of \(50\,\mathrm{N\,m^{-1}}\). The block is pulled to a distance \(x=10\,\mathrm{cm}\) from its equilibrium position at \(x=0\) on a frictionless surface from rest at \(t=0\). Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
Solution:
The block executes SHM. Angular frequency:
\[
\omega = \sqrt{\frac{k}{m}} = \sqrt{\frac{50}{1}} = 7.07\,\mathrm{rad\,s^{-1}}
\]
Displacement at any time \(t\):
\[
x(t) = 0.1 \cos(7.07 t)
\]
At \(x = 5\,\mathrm{cm} = 0.05\,\mathrm{m}\):
\(\cos(7.07 t) = 0.5\), so \(\sin(7.07 t) = \sqrt{3}/2 = 0.866\).
Velocity:
\[
v = -A\omega \sin(\omega t) = 0.1 \times 7.07 \times 0.866 = 0.61\,\mathrm{m\,s^{-1}}
\]
Kinetic energy:
\[
KE = \frac{1}{2}mv^2 = \frac{1}{2}\times1\times(0.6123)^2 = 0.19\,\mathrm{J}
\]
Potential energy:
\[
PE = \frac{1}{2}k x^2 = \frac{1}{2}\times 50 \times (0.05)^2 = 0.0625\,\mathrm{J}
\]
Total energy at \(x = 5\,\mathrm{cm}\):
\[
E = KE + PE = 0.19 + 0.0625 = 0.25\,\mathrm{J}
\]
At maximum displacement (\(x=10\,\mathrm{cm}\)), total energy is all potential:
\[
E = \frac{1}{2}kA^2 = \frac{1}{2}\times 50 \times (0.1)^2 = 0.25\,\mathrm{J}
\]
This confirms conservation of energy.