Horizontal Mass-Spring Harmonic Oscillator
Example
Question:
Two identical springs of spring constant \(k\) are attached to a block of mass \(m\) and to fixed supports as shown in Fig. 13.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
Solution:
Let the mass be displaced by a small distance \(x\) to the right side of the equilibrium position. Under this situation:
- The spring on the left side gets elongated by length \(x\)
- The spring on the right side gets compressed by the same length \(x\)
The forces acting on the mass are:
\[
F_1 = -kx \quad \text{(force by left spring, trying to pull mass towards mean position)}
\]
\[
F_2 = -kx \quad \text{(force by right spring, trying to push mass towards mean position)}
\]
The net force \(F\) acting on the mass is:
\[
F = -2kx
\]
Since the force is proportional to displacement and directed towards the mean position, the motion is simple harmonic.
The time period of oscillations is:
\[
T = 2\pi \sqrt{\frac{m}{2k}}
\]
System Information
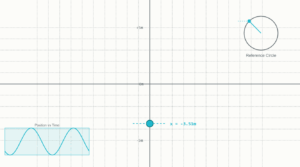
This simulation demonstrates a mass attached to two identical springs in a horizontal arrangement executing simple harmonic motion.
When displaced from equilibrium, the restoring force is:
F = -2kx
The theoretical period of oscillation is:
T = 2π√(m/2k)