Example

Question:

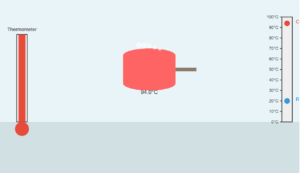
When 0.15 kg of ice at \(0^\circ\mathrm{C}\) is mixed with 0.30 kg of water at \(50^\circ\mathrm{C}\) in a container, the resulting temperature is \(6.7^\circ\mathrm{C}\). Calculate the heat of fusion of ice.
(\(s_\mathrm{water} = 4186\,\mathrm{J\,kg^{-1}\,K^{-1}}\))

Solution:

Heat lost by water: \[ Q_\mathrm{lost} = m_w s_w (\theta_f - \theta_{i,w}) = 0.30 \times 4186 \times (50.0 - 6.7) = 54,376.14\,\mathrm{J} \]
Heat required to melt ice: \[ Q_\mathrm{melt} = m_\mathrm{ice} L_f = 0.15\,L_f \]
Heat required to raise temperature of melted ice to final temperature: \[ Q_\mathrm{raise} = m_w s_w (\theta_f - \theta_{i,i}) = 0.15 \times 4186 \times (6.7 - 0) = 4,206.93\,\mathrm{J} \]
Heat lost = heat gained: \[ 54,376.14 = 0.15\,L_f + 4,206.93 \] \[ L_f = \frac{54,376.14 - 4,206.93}{0.15} = 333,795\,\mathrm{J\,kg^{-1}} \approx 3.34 \times 10^5\,\mathrm{J\,kg^{-1}} \]