Cooling Process Simulation
Visualizing Newton's Law of Cooling: How temperature changes over time based on the temperature difference with the surroundings
Value: 94 °C
Value: 20 °C
Value: 70
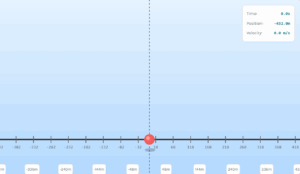
Simulation Results
Time to cool from 94°C to 86°C:
2.00 minutes
Time to cool from 71°C to 69°C:
0.70 minutes (42 seconds)
Current Temperature:
94.00 °C
Elapsed Time:
0.00 minutes
About Newton's Law of Cooling
Newton's Law of Cooling states that the rate of heat loss of a body is directly proportional to the difference in temperatures between the body and its surroundings. The law is often expressed as:
dT/dt = -k(T - Tₛ)
Where T is the temperature of the object, Tₛ is the surrounding temperature, and k is the cooling constant.
In the example problem, the pan cools from 94°C to 86°C in 2 minutes when the room temperature is 20°C. Using the formula, we can calculate that it will take 0.7 minutes (42 seconds) to cool from 71°C to 69°C.
